incastle의 콩나물
Chapter3. Fixed-Income Securities || Part2 본문
3.4 Yield
Yield
-
Interest rate implied by the payment structure
수익률 : 지불 구조에 따른 이자율 -
Interest rate at which the present value of the stream of payments (including coupon payments) is exactly equal to the current price
-
Yields are always quoted on an annual basis
- YTM(Yield to maturity) is the IRR of the bond at the current price
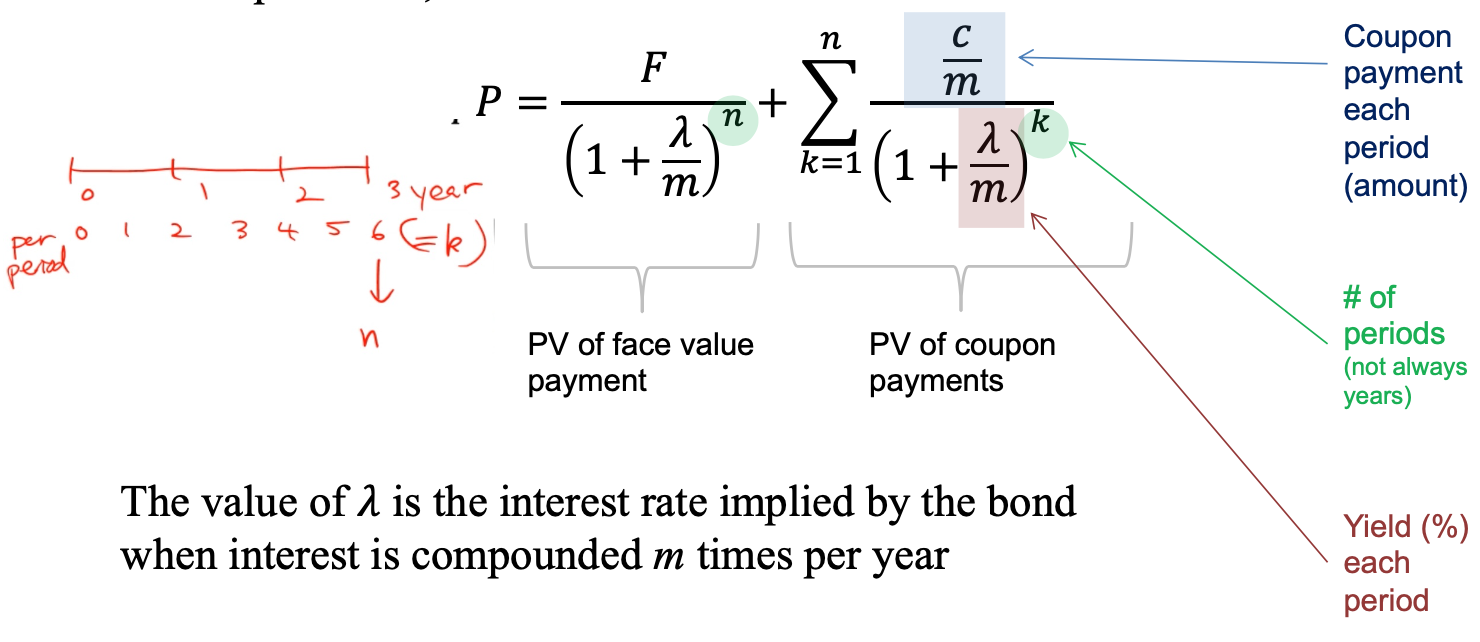
Bond Price
• Suppose that a bond with face value F makes m coupon payments of c/m each year (total of c each year) and there are n periods remaining. If the current price is P, the YTM is the value of 𝛌 such that
Price-Yield Relationship
- General interest rate environment urges the yield of every bond to conform to that of other bonds
이것이 바로 시장의 원리 - Yield of a bond can only change when bond’s price changesàAs yields move, prices move correspondingly
- Relationship between price and yield is shown by a price-yield curve
Price-Yield Curve

-
Negative slope -> Price and yield have an inverse relationship
-
If yield goes up, price goes down
-
Larger coupons result in steeper curves
- What is the bond price when yield is zero?
- When YTM = 0, bond is priced as if it offered no interest => Money in the future is not discounted so the present value is equal to the sum of all payments
- What is the bond price when yield and coupon rate are identical?
- Value of the bond is equal to the par value (par bonds = Face Value, 신기하다!!)

- As maturity is increased, the price-yield curve becomes steeper => Longer maturities imply greater sensitivity of price to yield
-
Suppose you purchase a 10% bond at par. It is likely that all bonds of maturity approximately 30 years would have yields of 10%. Then 10% would represent the market rate for such bonds.
-
Now suppose market conditions change and the yield increases to 11%. The price will drop to 91.28
-
With a 3-year 10% par bond, the price will drop to 97.50èInterest rate risk is lower
-
Yield Risk
-
If yields change, bond prices also change
-
Affects the near-term value (an immediate risk) => Price is governed by the price-yield curve
- Not affected if the bond is not sold
- Continue to receive the promised coupon payments and the face value at maturity
- Remains a fixed-income
3.5 Duration
Price and Maturity
-
Bonds with long maturities have steeper price-yield curves than bonds with short maturities
-
But maturity itself is not a complete quantitative measure of interest rate sensitivity
- Duration does give a direct measure of sensitivity
- '기울기가 크다'만으로 민감도를 측정하기가 어려움 => Duration 나옴
Duration
-
Weighted average of the times that payments (cash flows) are made
- Weighting coefficients are the present values of the individual cash flows
- Suppose cash flows are received at times t0, t1, ...., tn the duration is
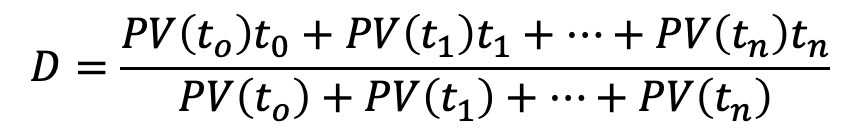
where PV(tk) is the present value of the cash flow that occurs at time tk
- Duration is the sensitivity of price with respect to changes in interest rate
=> Therefore, only cash flows defined from the bond is considered
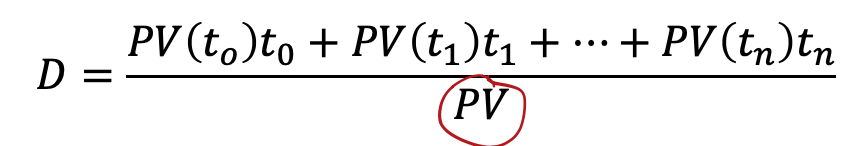
- where PV(tk) is the present value of the cash flow that occurs at time tk and PV is the total present value,

-
Duration is a weighted average of cash flow times => Has units of time(대부분 year)
- When cash flows are all nonnegative, then t0 ≤ D ≤ tn
=> Duration is a time intermediate between the first and the last cash flows - Consider a bond as multiple individual cash flows each at its maturity
=> Duration is an average of the maturities of all individual payments

- What is the duration of a zero-coupon bond?
- Zero-coupon bond has a duration equal to its maturity
- What about nonzero-coupon bonds?
- Nonzero-coupon bonds have durations strictly less than their maturity dates
Macaulay Duration
-
Macaulay duration : use yield for computing duration
- Suppose m payments are made each year where the payment in period k is ck and there are n periods remaining. Then, the Macaulay duration is
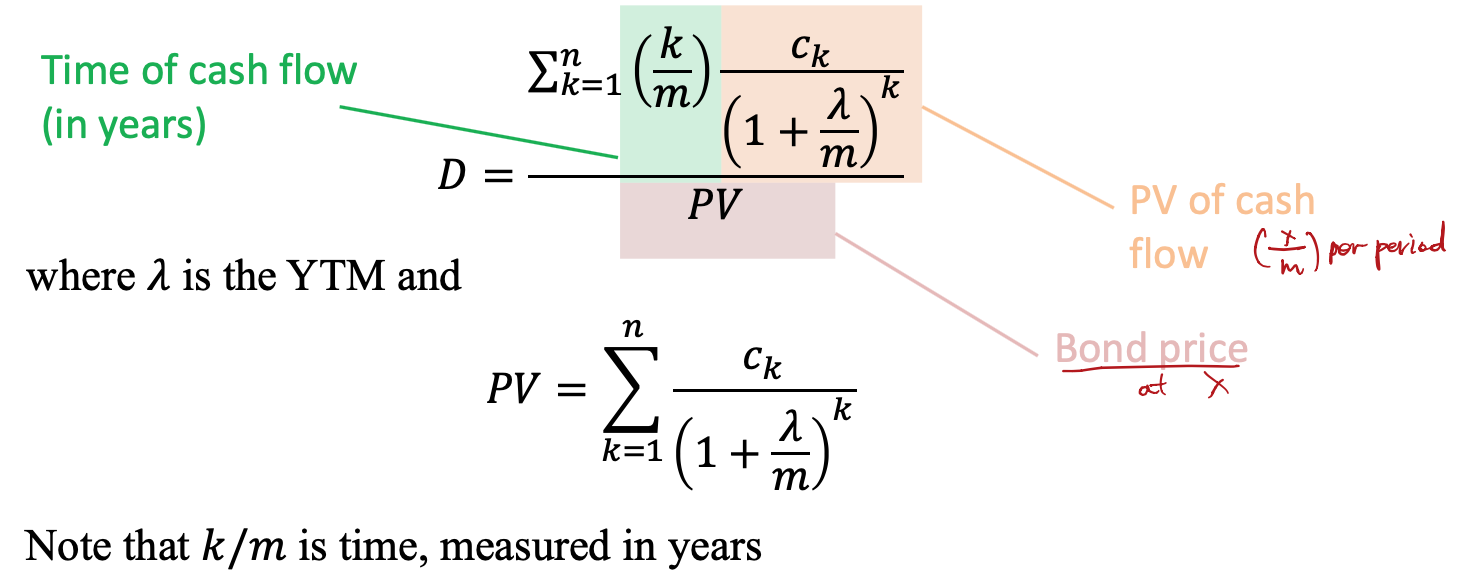

- 이렇게 공식으로 쓰기도 한다.

-
Duration is useful because it directly measures the sensitivity of price to changes in yield

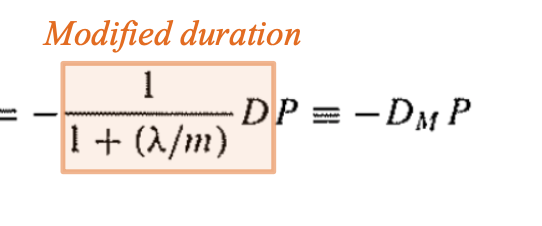
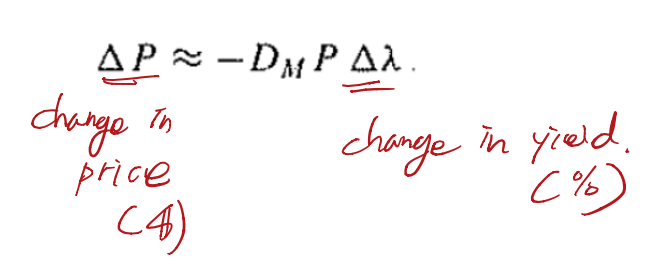
- Modified duration represents the percentage change in price of a bond per 1% point change in yield
- If a bond has a modified duration of 3 years
- This means that a 1% increase (0.01 increase) in interest rates will reduce the bond price by about 3%
Note the difference between Macaulay duration and modified duration
▫ Macaulay duration calculates the weighted average of cash flow periods, whereas modified duration derives the bond price sensitivity
'20-1 대학 수업 > 금융공학' 카테고리의 다른 글
| Chapter4. Term Structure of Interest Rate || Part.2 (0) | 2020.04.20 |
|---|---|
| Chapter4. Term Structure of Interest Rate || Part.1 (0) | 2020.04.17 |
| Chapter3. Fixed-Income Securities || Part1 (0) | 2020.04.14 |
| Chapter2. The Basic Theory of Interest || Part2 (0) | 2020.04.13 |
| Chapter2. The Basic Theory of Interest || Part1 (0) | 2020.04.12 |




