incastle의 콩나물
[금융데이터분석] Historical Returns :: Part 2 본문
Log Returns

- Return값에 log를 씌운 것이다.
- continuous compounding의 수익률이 발생할 때의 값과 같다.
- simple return vs log return
- 0% 일 때만 값이 비슷함
- portfolio return을 계산할 때는 simple return을 사용해야 한다.
- 개별 주식의 log return들의 weighted average는 전체 포트폴리오의 log를 씌운 것과 같지 않다. (수식을 생각하면 당연하지)
- 그런데 return들이 작으면, 크게 차이는 안 난다.
- investment의 performance를 이야기할 때는 log return을 사용하곤 한다.
- Compounded return is valuable when evaluating performance
Frequency
- Long-term analysis => monthly return
- year or so => weekly return
- But if the number of candidate assets increase, we need more returns => daily return
- monthly를 yearly or daily 등과 같이 변환하고 싶으면?
- if we further assume that monthly returns가 (독립적 + 같은 분포)
- each monthly return r_i 이는 같은 기댓값을 갖는다. 따라서
- if we further assume that monthly returns가 (독립적 + 같은 분포)
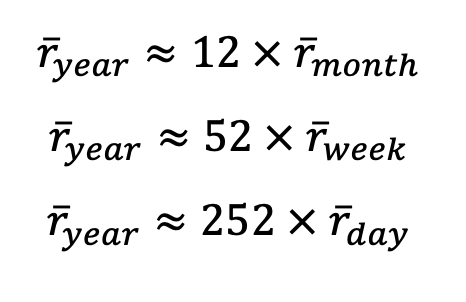
- 그리고 (독립적 + 같은 분포) 이니까 cov도 0이어서
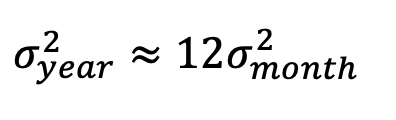
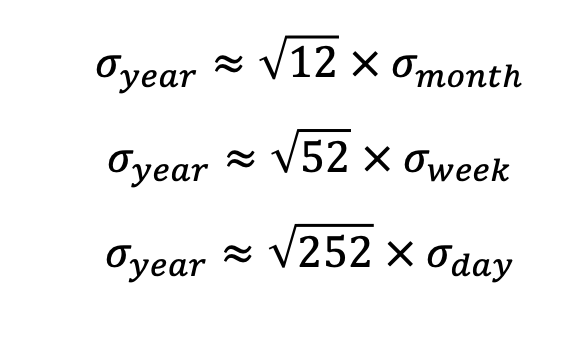
Volatility Conversion
- 투자 기간이 길면 길수록 변동성은 줄어든다.
Return Distribution
- 우리는 이미 주식 수익률이 정규 분포에 비해 꼬리가 더 두껍다는 것에 대해 이미 이야기했습니다.
- 이걸 측정하는 방법들
- QQ plot, K-S test, J-B test(sample size가 커야한다)
K-S Test
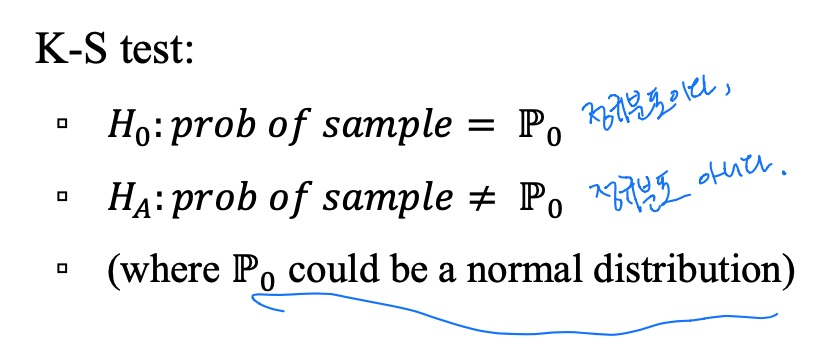
- Compare empirical cdf(경험적 cdf) with the cdf of normal distribution.
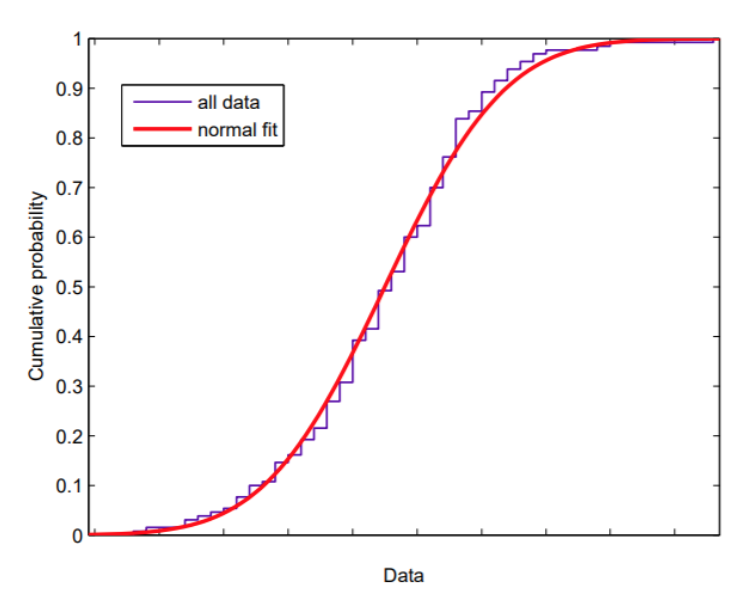
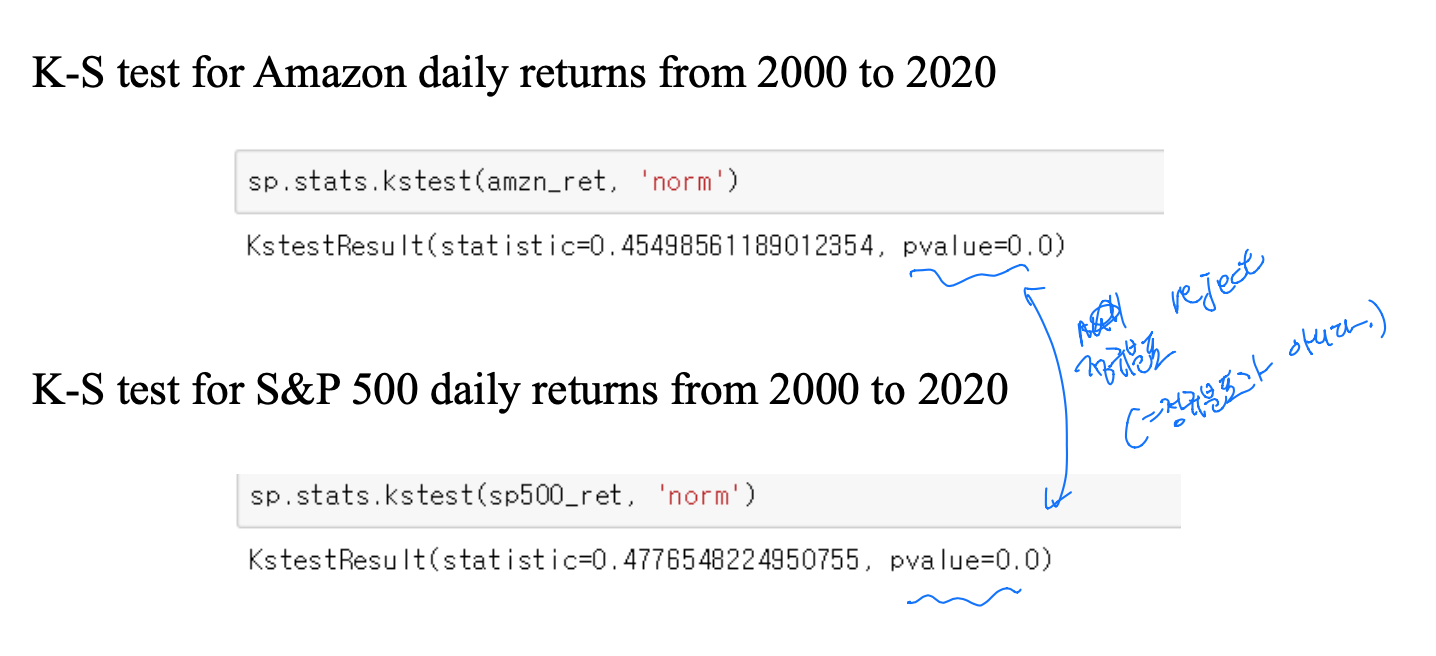
Stock vs Stock Market
- 일반적으로 개별 주식의 skewness는 양수(positive)이고 시장 전체는 음수(negative)하다.
'20-2 대학수업 > 금융데이터분석' 카테고리의 다른 글
| [금융데이터분석] Factor Models :: Part.2 (0) | 2020.10.10 |
|---|---|
| [금융데이터분석] Factor Models :: Part.1 (0) | 2020.10.08 |
| [금융데이터분석] Historical Returns :: Part1 (0) | 2020.10.05 |
Comments



