incastle의 콩나물
[금융데이터분석] Factor Models :: Part.1 본문
- Single Factor Models
- most widely recognized single factor model is the CAPM(capital asset pricing model)
- CAPM
- CAPM hypothesizes the following relationship between the expected excess return on any single risky asset and the expected excess return on the market portfolio
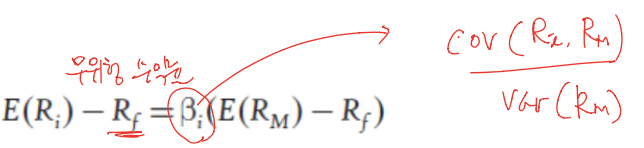

-
Value of 𝛽𝑖 is referred to as the beta of an asset
-
The value (r_i - r_f) is termed the expected excess rate of return of asset i => Amount by which the return is expected to exceed the risk-free rate
risk free asset 보다는 asset i 가 돈을 더 많이 벌어야 할 것 아니냐? 그래서 ri-rf가 중요함 -
In summary, CAPM says that the expected excess return of an asset is proportional to the expected excess return of the market portfolio, and the proportionality factor is 𝛽
요약하면, CAPM은 자산의 예상 초과 수익률은 시장 포트폴리오의 예상 초과 수익률에 비례하며, 비례 계수는 𝛽입니다. - CAPM은 또한 자산의 예상 초과 수익이 시장과의 공분산에 정비례한다고 말합니다.(𝛽의 수식을 생각하면 okay)
Betas of Common Stocks
-
Unless there are drastic changes in a company's situation, its beta tends to be relatively stable
- Generally, aggressive companies or highly leveraged companies have high betas, whereas conservative companies whose performance is unrelated to the general market behavior are expected to have low betas
- Companies in the same business are expected to have similar betas (but not identical)
Single Factor Models
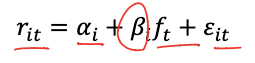



- expected return 구할 때 error의 평균은 0이라고 위에서 가정했으니까 날아감
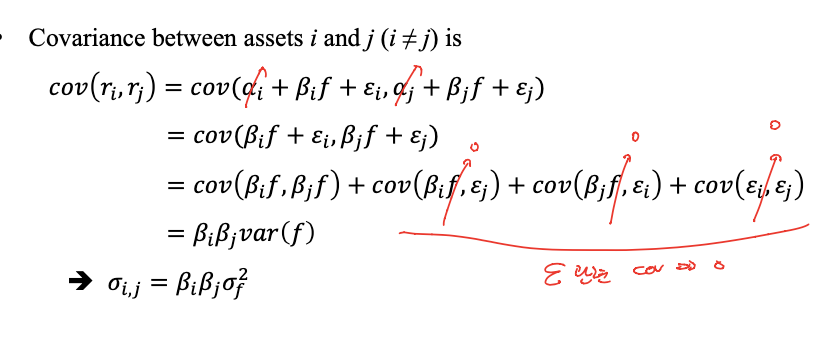

- 에러의 분산 => factor로 표현할 수 없는 risk // 시장의 전체 흐름으로는 설명할 수는 없고, 개별 주식의 고유한 움직인, 특징을 나타내는 risk
Single Factor Models OLS Estimates
OLS(Ordinary least squares)

- 베타0, 베타 1을 찾아야 한다. 그러기 위해서 Q값을 minimize 한다.
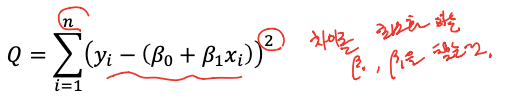
- 편미분 해서 요리조리하면 찾을 수 있음
- 그냥 엑셀에서 y=ax+b 찾으면, intercept가 베타 0이고 기울기가 베타 1
Single Factor Models :: EWMA Estimates
- 베타를 구할 때 최근의 데이터를 더 반영하기 위한 방법이 필요하다! 기간 전체로 구할 것이 아니라. => weighted moving average
- 단기적으로 의사결정이 필요할 때 유용함
- exponentially-weighted moving average (EWMA) model

-
Setting 𝜆 = 0.95 corresponds to a half-life of about 25 days (상황에 따라서 최근 것에 더 높은 가중치를 주고 싶으면 더 낮은 람다를 넣어준다.)
EWMA
- 만약 사용하는 기간이 꽤 길다면, 무한대로 기간을 생각하면
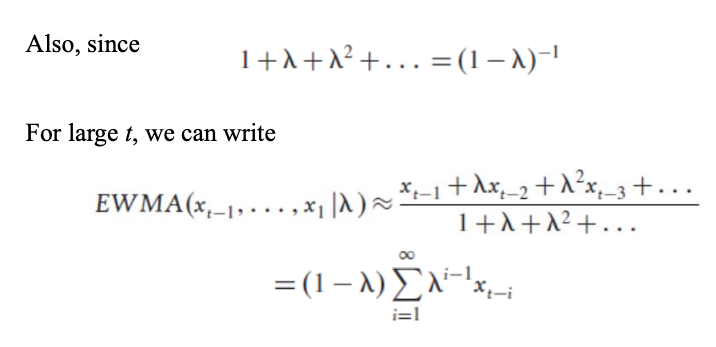
- 기간을 무한으로 해서 sum을 하니까 분모의 값을 앞으로 (1-람다)로 뺄 수 있음
- 분산과 공분산을 계산할 수 있음
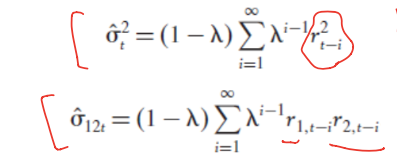
- 무한대로 안 하고 period가 3이라면 아래와 같겠지
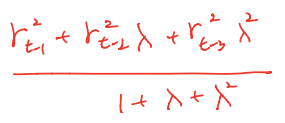
- 그래서 EWMA를 사용해서 베타를 구하면 아래오 같아짐
- 최근 시장의 상황을 더욱 반영하는 모습!

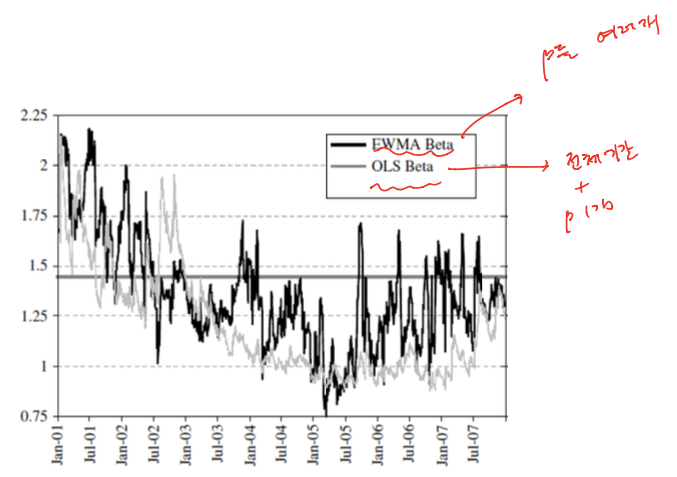
Single-Factor Model : Portfolios
- weight가 정해져 있을 때 weight를 곱해서 포트폴리오의 수익률을 정한다
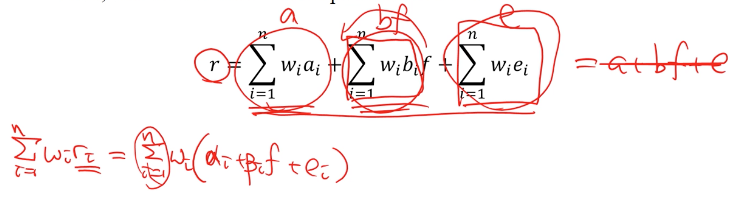
- 포트폴리오의 베타도 마찬가지로 weight를 곱해서 sum 한다.
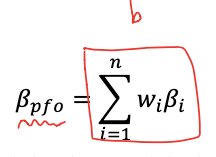
- Portfolio Risk & variance

'20-2 대학수업 > 금융데이터분석' 카테고리의 다른 글
| [금융데이터분석] Factor Models :: Part.2 (0) | 2020.10.10 |
|---|---|
| [금융데이터분석] Historical Returns :: Part 2 (0) | 2020.10.06 |
| [금융데이터분석] Historical Returns :: Part1 (0) | 2020.10.05 |
Comments