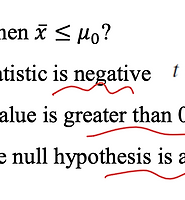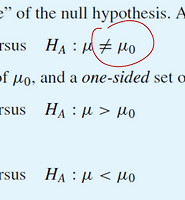incastle의 콩나물
[응용통계학] Chapter 8-1. Inferences on a Population Mean 본문
8장에서 배울거 : Confidence intervals(신뢰구간) | Hypothesis testing(가설 검정)
Sample Data
- unknown continuos probability distribution에서 independent observation을 뽑은 것
Confidence Interval
- Confidence interval for μ is an interval that contains plausible values of the parameter μ
- μ에 대한 신뢰 구간은 매개 변수 μ의 그럴듯한 값을 포함하는 구간입니다.
- 무언가를 추정하는 것=> 표준 편차도 그런 의미였다.
- but, 표준편차는 점추정치이고, 신뢰 구간은 추정의 '구간'임
- Confidence interval is associated with a confidence level
- ex) population mean이 특정 구간에 속할 확률이 90%이다. <=> 이런 식으로 사용 됨
- Confidence interval : unknown 파라미타가 있는 구간
- Confidence level : 실제값이 그 안에 있을 확률
t-intervals
- Implementation of t-intervals requires that the sample mean be an observation from a normal distribution
- t-interval을 구현하려면 표본 평균이 정규 분포의 관측치 여야합니다.
- 그런데 central limit theorem에(CLT) 따르면 sample size가 30개 이상이면 보통 정규분포를 근사한다고 가정한다.
따라서 t-interval을 적용하기 위해서는
- 정규분포 이거나
- sample size가 30개 보다 크거나 해야한다.
- 두 가지에 해당 안될때 t-interval 사용법(nonparametric technique이란 게 있음)은 챕터 15에서 두둥등장
- confidence level을 알고 있을 때 confidence interval을 계산하는 법(아래 그림)

- 여기서 x bar는 점 추정치, t_a/2는 critical point, s/root(n) 은 standard error이다.
- 실제 평균과 점추정치가 같을 때 당연히 최고이지만, 우리는 추정을 하는 것이니까 Critical point(t_a/2) * standard deviation을 더하고 빼서 구간을 만든 거임

- 이 interval을 two-sided t-interval or variance unknown confidence interval 이라고 부른다
Length of t-intervals
- confidence interval의 길이를 구하는 것은 매우 간단

- critical point * s.e * 2배
- standard error가 감소할수록, length가 줄어들고, 실제 평균과 점추정치가 비슷해진다.
- 또한 confidence level(1-a)이 증가 할수록, a(알파)는 감소하고
- critical point는 증가하고, 따라서 confidence interval은 길어진다.

- Higher confidence levels require longer confidence

** confidence interval 안에 모집단의 평균이 있다는 것이지, 실제 데이터가 confidence interval에 존재한다는 것은 아니다.
'20-2 대학수업 > 응용통계학' 카테고리의 다른 글
| [응용통계학] Chapter 9-1. Comparing Two Population Means (0) | 2020.10.10 |
|---|---|
| [응용통계학] Chapter 8-4. Inferences on a Population Mean (0) | 2020.10.09 |
| [응용통계학] Chapter 8-3. Inferences on a Population Mean (0) | 2020.10.08 |
| [응용통계학] Chapter 8-2. Inferences on a Population Mean (0) | 2020.10.05 |
Comments