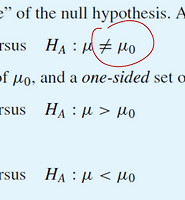incastle의 콩나물
[응용통계학] Chapter 8-4. Inferences on a Population Mean 본문
Two Sided t-Test
** p-value를 구하는 것과 t-static을 구하는 것을 구분하라
- -|t| 값보다 작거나 +|t|값보다 클 때 => worse than the observed data set
One Sided t-Test
- H0를 u <= u0라고 설정했다면(observe가 더 클 거야) => observe가 더 클 확률 => t값보다 클 때 worse data set


- t-static 기준으로 오른쪽에 있는 면적을 쫙~ 색칠해서 이 면적의 넓이 = p-value
- 면적이 얼마나 되느냐~에 따라서 null hypothesis를 accept 할 것이냐~ reject 할 것이냐 결정

t-test 절차
- 무엇을 보이고자 하느냐?
- 귀무 가설/ 대립 가설 설정
- t 값 계산
- p-value 계산
- 평가
Significance Levels (유의 수준)
- Hypothesis test can be defined formally in terms of a significance level α
- rejects the null hypothesis 𝐻_0 if a p-value smaller than α is obtained, and
- accepts the null hypothesis 𝐻_0 if a p-value larger than α is obtained
- p-value < a ==> reject H0
- p-value > a ==> accept H0
- p-value는(confidence interval) significance level을 아는 것보다 더 많은 정보를 제공한다. 유의 수준 α는 귀무가설을 허용하거나 기각할 뿐이다.

- 이번에는 one-sided problem

'20-2 대학수업 > 응용통계학' 카테고리의 다른 글
| [응용통계학] Chapter 9-1. Comparing Two Population Means (0) | 2020.10.10 |
|---|---|
| [응용통계학] Chapter 8-3. Inferences on a Population Mean (0) | 2020.10.08 |
| [응용통계학] Chapter 8-2. Inferences on a Population Mean (0) | 2020.10.05 |
| [응용통계학] Chapter 8-1. Inferences on a Population Mean (0) | 2020.09.30 |