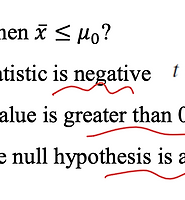incastle의 콩나물
[응용통계학] Chapter 8-3. Inferences on a Population Mean 본문
Hypothesis Testing 1
- Hypothesis Test를 통해 실험자는 특정 진술 또는 가설의 타당성 또는 신뢰성을 평가할 수 있습니다.
- Hypothesis testing은 2개의 statements를 포함한다.
- Null hypothesis(귀무가설)
- Alternative hypothesis(대립 가설)

p-Value
- Plausibility of a null hypothesis is measured with a p-value
- p-value가 작을수록 null hypothesis의 타당성은 줄어들고 => not null(alternative를 선택한다)
- p-value는 확률이다.
- null hypothesis에 해당하는 데이터가 obseved 될 확률

- 0.01보다 작으면
- H0는 not plausible 하다.
- 따라서 H0를 기각한다.
- HA가 true라고 고려한다.
- the null hypothesis is said to have been rejected in favor of the alternative hypothesis
- 0.01보다 크면
- H0는 accepte 한다
- H0 is plasuble( But H0 is not proven)
- 0.01과 0.1 사이라면
- Experment is inconclusive
- 결론을 내리기 어렵다로 해석
Hypothesis Testing 2
- 맞다고 보이고 싶은 것을 alternative에 둔다.
Calculation of p-Value( Two-sided hypothesis)
- data set과 null hypothsis의 불일치를 측정할 때는 t-statistic을 사용한다.

- x와 u가 같으면 t=0이다(일치한다.)
- t값이 올라가면 discrepancy(불일치)도 올라간다.
- p-value를 계산하기 위해서는


- 그런데 t분포는 대칭적이니까 그냥

- 2배 해서 찾아도 괜찮음
'20-2 대학수업 > 응용통계학' 카테고리의 다른 글
| [응용통계학] Chapter 9-1. Comparing Two Population Means (0) | 2020.10.10 |
|---|---|
| [응용통계학] Chapter 8-4. Inferences on a Population Mean (0) | 2020.10.09 |
| [응용통계학] Chapter 8-2. Inferences on a Population Mean (0) | 2020.10.05 |
| [응용통계학] Chapter 8-1. Inferences on a Population Mean (0) | 2020.09.30 |