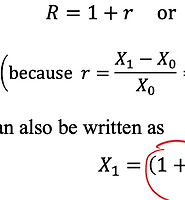incastle의 콩나물
Chapter 6. Mean-Variance Portfolio Theory || Part 3 본문
Diagram of a Portfolio
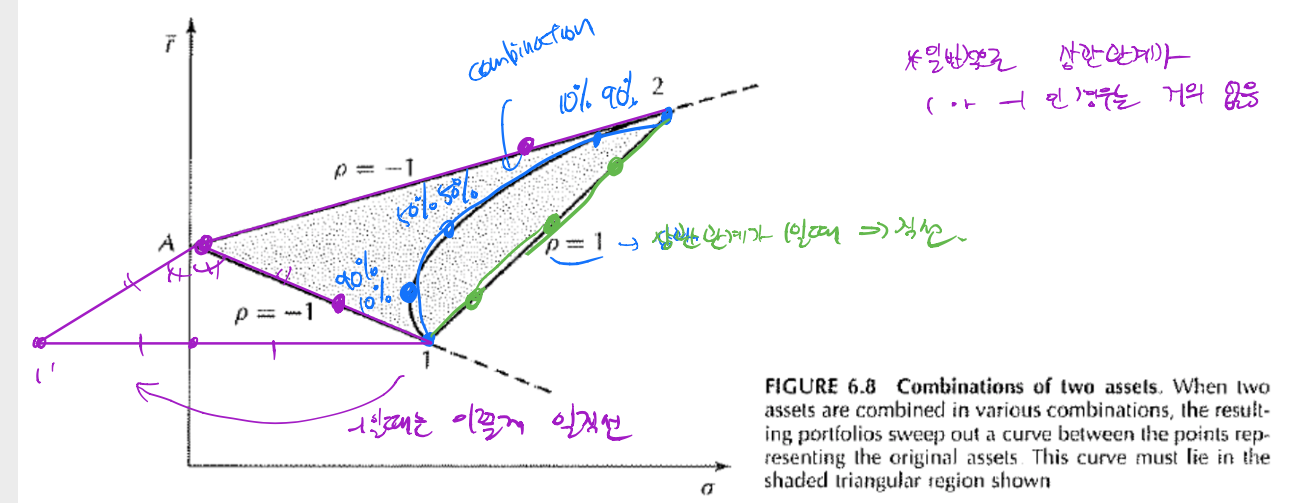
- Combinations of assets 1 and 2 trace out a curve that includes the two assets
- Exact shape of the curve depends on the covariance of assets 1 and 2
- Solid portion corresponds to positive combinations of the two assets
6.5 The Feasible Set
Feasible Set
- Suppose that there are n basic assets
- We can plot them as points on the mean-standard deviation diagram
- Next imagine forming portfolios from these n assets, using every possible weighting scheme
- Hence, there are portfolios consisting of each of the n assets alone, combinations of two assets, combinations of three, and so forth
- These portfolios are made by letting the weighting coefficients w_i range over all possible combinations
이 포트폴리오는 모든 가능한 조합에 대한 가중 계수 w_i 범위를 허용함으로써 만들어집니다 - Set of points that correspond to portfolios is called the feasible set or feasible region
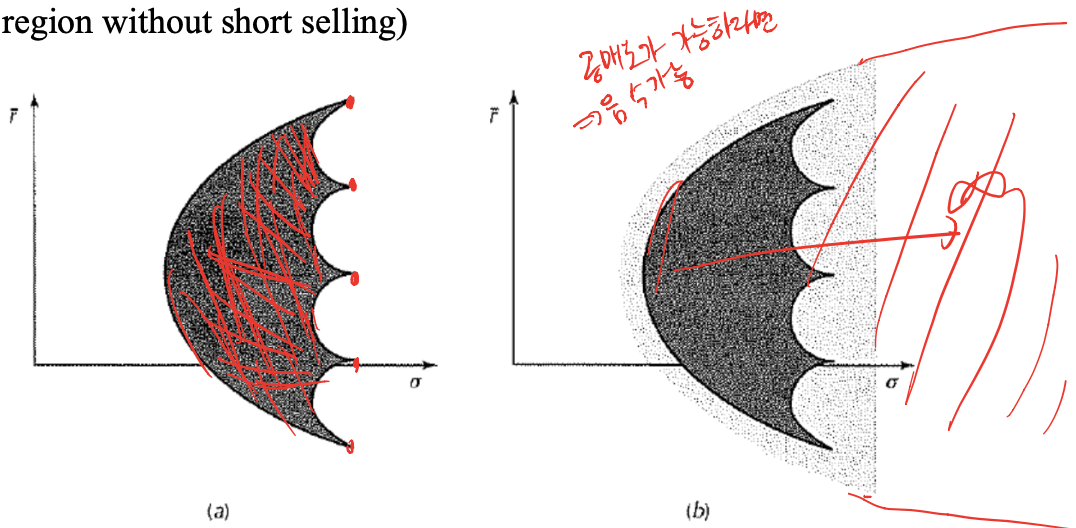
Asset이 3개 있을 때(not perfectly correlated and with different mean)
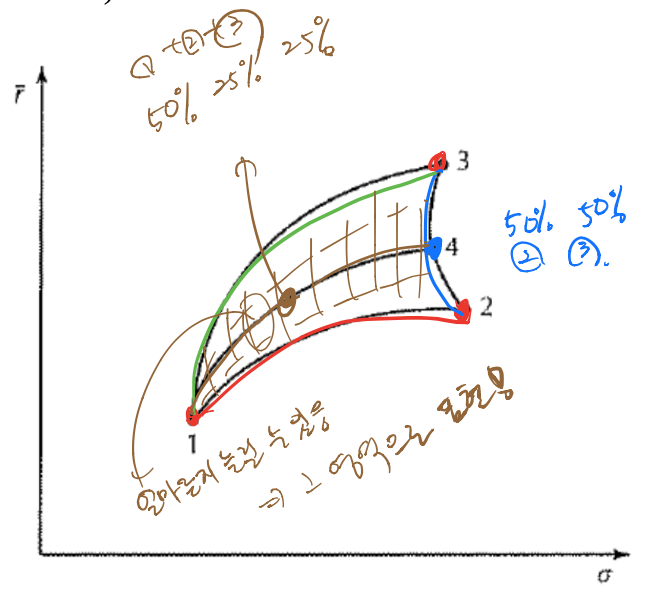
Feasible Set
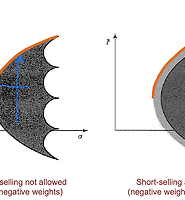
- Feasible region is convex to the left
- Feasible region is shaped differently based on whether short selling of assets is allowed or not allowed
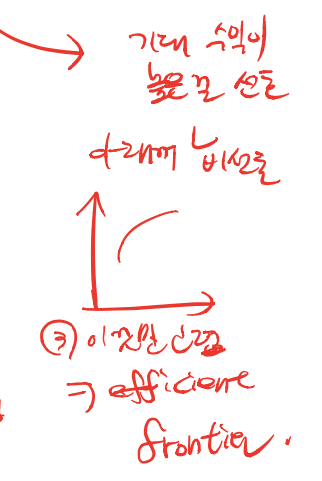
Minimum-Variance Set
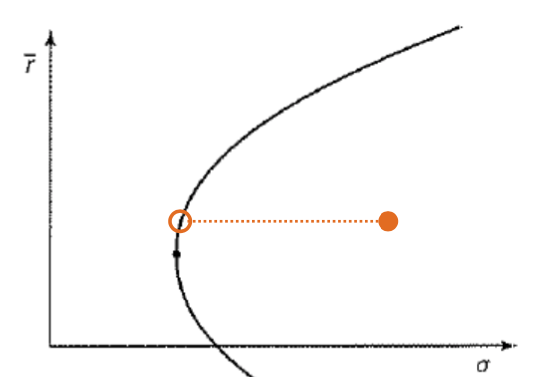
- Left boundary of a feasible set is called the minimum-variance set
-
For any value of the mean rate of return, the feasible point with the smallest variance (or standard deviation) is the corresponding left boundary point
-
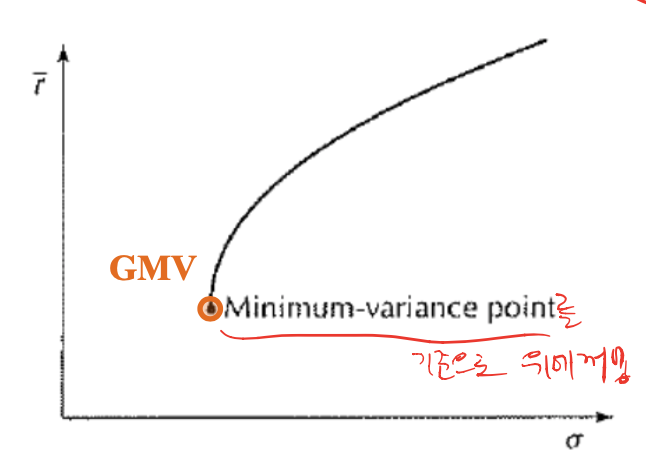
There is a special point on this set having minimum variance => Minimum-variance point or global minimum-variance (GMV) portfolio

Risk Aversion
- For a given mean rate of return, most investors will prefer the portfolio corresponding to the leftmost point on the line
- ==> Point with the smallest standard deviation for the given mean
- An investor who agrees with this viewpoint is said to be risk averse(리스크 싫엉)
- An investor who would select a point other than the one of minimum standard deviation is said to be risk preferring (or risk seeking)
minimum standard 이외에 다른 지점을 투자하면 => risk preferring
-
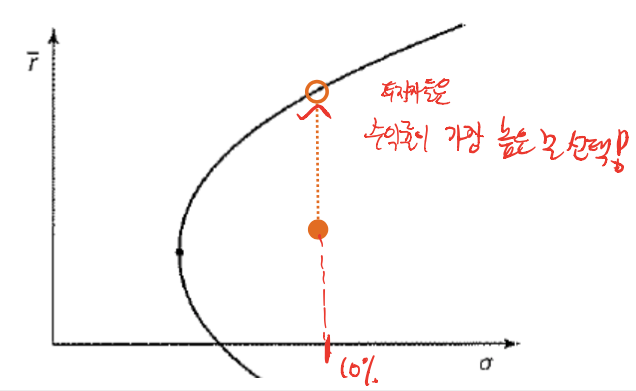
We can turn the argument around 90 degrees and consider portfolios corresponding to the various points on a vertical line (portfolios with a fixed standard deviation and various mean values)
-
Most investors will prefer the highest point on such a linea => Select the largest mean for a given level of standard deviation
-
This arguments imply that only the upper part of the minimum-variance set will be of interest to investors
- Upper portion of the minimum-variance set is termed the efficeint frontier of the feasible region

'20-1 대학 수업 > 금융공학' 카테고리의 다른 글
| Chapter7. The Capital Asset Pricing Model (0) | 2020.05.17 |
|---|---|
| Chapter 6. Mean-Variance Portfolio Theory || Part 4 (0) | 2020.05.17 |
| Chapter 6. Mean-Variance Portfolio Theory || Part 1 (0) | 2020.05.16 |
| Chapter4. Term Structure of Interest Rate || Part.3 (0) | 2020.04.20 |
| Chapter4. Term Structure of Interest Rate || Part.2 (0) | 2020.04.20 |