incastle의 콩나물
Chapter 6. Mean-Variance Portfolio Theory || Part 4 본문
6.6 The Markowitz Model (mean-variance model, analysis라고도 불림)
Assumptions of the M-V model
- Assumptions of the mean-variance approach
- 모든 투자자들은 mean(Return)과 variance(risk)만을 고려한다.
- 모든 투자자는 평균, 분산 및 공분산에 대해 동일한 평가를 합니다
- All investors are rational (= risk averse)
- investors only consider a single-period framework
Markowitz Model
-
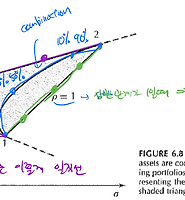
We will now formulate a mathematical problem that leads to minimum variance portfolios
이제 최소 분산 포트폴리오로 이어지는 수학적 문제를 공식화 할 것입니다 - n개의 asset이 있고, 각각의 수익률 r과 공분산이 존재한다. 각각의 asset에 w_i만큼 weight를 줘서 투자를 한다.(당연히 weight의 합은 1이다.)
- 우리가 얻고자 하는 수익률 r을 정하고, 이 r을 달성하기 위한 가장 작은 variance를 갖는 지점을 찾는다.

한글을 영어로 풀어서 쓰면은 아래와 같음


이 공식은 아래와 같이 새로운 식으로 재정의 됨

만약에 r에 상관없이 risk가 가장 작은 portfolio를 찾아야 한다면?(Global minimum-variance portfolio)

6.8 Inclusion of a Risk Free Asset
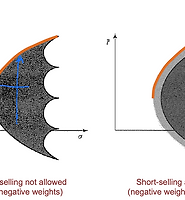
지금까지는 n개의 자산이 있다고 가정할 때, 이 자산들이 전부 위험 자산이었음(표준편차가 0보다 큰)
그런데 무위험 자산도 투자 대상중 하나이면 어떻게 될까?
Risk-Free Asset
- Risk-Free asset has a return that is deterministic(known with certainty) and therefore has 표준편차=0
-
Its inclusion in a portfolio corresponds to lending or borrowing cash at the risk-free rate
-
Inclusion of a risk-free asset in the list of possible assets is necessary because investors have the opportunity to borrow or lend


-
These equations show that both the mean and the standard deviation of the portfolio vary linearly with 알파
-
This means that as 알파 varies, the point representing the portfolio traces out a straight line in the mean-standard deviation plane


6.9 The One-Fund Theorem
-
When risk-free borrowing and lending are available, the efficient set consists of a single straight line
- There will be a point F in the original feasible set that is on the line segment defining the overall efficient set
- Any efficient point can be expressed as a combination of this asset and the risk-free asset
One-fund theorem : There is a single portfolio (fund) F of risky assets such that any efficient portfolio can be constructed as a combination of the fund F and the risk-free asset

'20-1 대학 수업 > 금융공학' 카테고리의 다른 글
| Chapter7. The Capital Asset Pricing Model || Part.2 (5) | 2020.05.18 |
|---|---|
| Chapter7. The Capital Asset Pricing Model (0) | 2020.05.17 |
| Chapter 6. Mean-Variance Portfolio Theory || Part 3 (0) | 2020.05.17 |
| Chapter 6. Mean-Variance Portfolio Theory || Part 1 (0) | 2020.05.16 |
| Chapter4. Term Structure of Interest Rate || Part.3 (0) | 2020.04.20 |